News classification with topic models in gensim¶
News article classification is a task which is performed on a huge scale by news agencies all over the world. We will be looking into how topic modeling can be used to accurately classify news articles into different categories such as sports, technology, politics etc.
Our aim in this tutorial is to come up with some topic model which can come up with topics that can easily be interpreted by us. Such a topic model can be used to discover hidden structure in the corpus and can also be used to determine the membership of a news article into one of the topics.
For this tutorial, we will be using the Lee corpus which is a shortened version of the Lee Background Corpus. The shortened version consists of 300 documents selected from the Australian Broadcasting Corporation's news mail service. It consists of texts of headline stories from around the year 2000-2001.
Accompanying slides can be found here.
Requirements¶
In this tutorial we look at how different topic models can be easily created using gensim. Following are the dependencies for this tutorial:
- Gensim Version >=0.13.1 would be preferred since we will be using topic coherence metrics extensively here.
- matplotlib
- Patterns library; Gensim uses this for lemmatization. ONLY FOR PYTHON 2.5+ - no support for Python 3 yet.
- nltk.stopwords
- pyLDAVis
We will be playing around with 4 different topic models here:
- LSI (Latent Semantic Indexing)
- HDP (Hierarchical Dirichlet Process)
- LDA (Latent Dirichlet Allocation)
- LDA (tweaked with topic coherence to find optimal number of topics) and
- LDA as LSI with the help of topic coherence metrics
First we'll fit those topic models on our existing data then we'll compare each against the other and see how they rank in terms of human interpretability.
All can be found in gensim and can be easily used in a plug-and-play fashion. We will tinker with the LDA model using the newly added topic coherence metrics in gensim based on this paper by Roeder et al and see how the resulting topic model compares with the exsisting ones.
import os
import re
import operator
import matplotlib.pyplot as plt
import warnings
import gensim
import numpy as np
warnings.filterwarnings('ignore') # Let's not pay heed to them right now
from gensim.models import CoherenceModel, LdaModel, LsiModel, HdpModel
from gensim.models.wrappers import LdaMallet
from gensim.corpora import Dictionary
from pprint import pprint
%matplotlib inline
test_data_dir = '{}'.format(os.sep).join([gensim.__path__[0], 'test', 'test_data'])
lee_train_file = test_data_dir + os.sep + 'lee_background.cor'
Analysing our corpus.
- The first document talks about a bushfire that had occured in New South Wales.
- The second talks about conflict between India and Pakistan in Kashmir.
- The third talks about road accidents in the New South Wales area.
- The fourth one talks about Argentina's economic and political crisis during that time.
- The last one talks about the use of drugs by midwives in a Sydney hospital.
Our final topic model should be giving us keywords which we can easily interpret and make a small summary out of. Without this the topic model cannot be of much practical use.
with open(lee_train_file) as f:
for n, l in enumerate(f):
if n < 5:
print([l])
def build_texts(fname):
"""
Function to build tokenized texts from file
Parameters:
----------
fname: File to be read
Returns:
-------
yields preprocessed line
"""
with open(fname) as f:
for line in f:
yield gensim.utils.simple_preprocess(line, deacc=True, min_len=3)
train_texts = list(build_texts(lee_train_file))
len(train_texts)
Preprocessing our data. Remember: Garbage In Garbage Out¶
"NLP is 80% preprocessing."
-Lev Konstantinovskiy
This is the single most important step in setting up a good topic modeling system. If the preprocessing is not good, the algorithm can't do much since we would be feeding it a lot of noise. In this tutorial, we will be filtering out the noise using the following steps in this order for each line:
- Stopword removal using NLTK's english stopwords dataset.
- Bigram collocation detection (frequently co-occuring tokens) using gensim's Phrases. This is our first attempt to find some hidden structure in the corpus. You can even try trigram collocation detection.
- Lemmatization (using gensim's
lemmatize) to only keep the nouns. Lemmatization is generally better than stemming in the case of topic modeling since the words after lemmatization still remain understable. However, generally stemming might be preferred if the data is being fed into a vectorizer and isn't intended to be viewed.
bigram = gensim.models.Phrases(train_texts) # for bigram collocation detection
bigram[['new', 'york', 'example']]
from gensim.utils import lemmatize
from nltk.corpus import stopwords
stops = set(stopwords.words('english')) # nltk stopwords list
def process_texts(texts):
"""
Function to process texts. Following are the steps we take:
1. Stopword Removal.
2. Collocation detection.
3. Lemmatization (not stem since stemming can reduce the interpretability).
Parameters:
----------
texts: Tokenized texts.
Returns:
-------
texts: Pre-processed tokenized texts.
"""
texts = [[word for word in line if word not in stops] for line in texts]
texts = [bigram[line] for line in texts]
texts = [[word.split('/')[0] for word in lemmatize(' '.join(line), allowed_tags=re.compile('(NN)'), min_length=3)] for line in texts]
return texts
train_texts = process_texts(train_texts)
train_texts[5:6]
Finalising our dictionary and corpus
dictionary = Dictionary(train_texts)
corpus = [dictionary.doc2bow(text) for text in train_texts]
Topic modeling with LSI¶
This is a useful topic modeling algorithm in that it can rank topics by itself. Thus it outputs topics in a ranked order. However it does require a num_topics parameter (set to 200 by default) to determine the number of latent dimensions after the SVD.
lsimodel = LsiModel(corpus=corpus, num_topics=10, id2word=dictionary)
lsimodel.show_topics(num_topics=5) # Showing only the top 5 topics
lsitopics = lsimodel.show_topics(formatted=False)
hdpmodel = HdpModel(corpus=corpus, id2word=dictionary)
hdpmodel.show_topics()
hdptopics = hdpmodel.show_topics(formatted=False)
Topic modeling using LDA¶
This is one the most popular topic modeling algorithms today. It is a generative model in that it assumes each document is a mixture of topics and in turn, each topic is a mixture of words. To understand it better you can watch this lecture by David Blei. Let's choose 10 topics to initialize this.
ldamodel = LdaModel(corpus=corpus, num_topics=10, id2word=dictionary)
pyLDAvis is a great way to visualize an LDA model. To summarize in short, the area of the circles represent the prevelance of the topic. The length of the bars on the right represent the membership of a term in a particular topic. pyLDAvis is based on this paper.
import pyLDAvis.gensim
pyLDAvis.enable_notebook()
pyLDAvis.gensim.prepare(ldamodel, corpus, dictionary)
ldatopics = ldamodel.show_topics(formatted=False)
Finding out the optimal number of topics¶
Introduction to topic coherence:
Topic coherence in essence measures the human interpretability of a topic model. Traditionally perplexity has been used to evaluate topic models however this does not correlate with human annotations at times. Topic coherence is another way to evaluate topic models with a much higher guarantee on human interpretability. Thus this can be used to compare different topic models among many other use-cases. Here's a short blog I wrote explaining topic coherence:
What is topic coherence?
def evaluate_graph(dictionary, corpus, texts, limit):
"""
Function to display num_topics - LDA graph using c_v coherence
Parameters:
----------
dictionary : Gensim dictionary
corpus : Gensim corpus
limit : topic limit
Returns:
-------
lm_list : List of LDA topic models
c_v : Coherence values corresponding to the LDA model with respective number of topics
"""
c_v = []
lm_list = []
for num_topics in range(1, limit):
lm = LdaModel(corpus=corpus, num_topics=num_topics, id2word=dictionary)
lm_list.append(lm)
cm = CoherenceModel(model=lm, texts=texts, dictionary=dictionary, coherence='c_v')
c_v.append(cm.get_coherence())
# Show graph
x = range(1, limit)
plt.plot(x, c_v)
plt.xlabel("num_topics")
plt.ylabel("Coherence score")
plt.legend(("c_v"), loc='best')
plt.show()
return lm_list, c_v
%%time
lmlist, c_v = evaluate_graph(dictionary=dictionary, corpus=corpus, texts=train_texts, limit=10)
pyLDAvis.gensim.prepare(lmlist[2], corpus, dictionary)
lmtopics = lmlist[5].show_topics(formatted=False)
LDA as LSI¶
One of the problem with LDA is that if we train it on a large number of topics, the topics get "lost" among the numbers. Let us see if we can dig out the best topics from the best LDA model we can produce. The function below can be used to control the quality of the LDA model we produce.
def ret_top_model():
"""
Since LDAmodel is a probabilistic model, it comes up different topics each time we run it. To control the
quality of the topic model we produce, we can see what the interpretability of the best topic is and keep
evaluating the topic model until this threshold is crossed.
Returns:
-------
lm: Final evaluated topic model
top_topics: ranked topics in decreasing order. List of tuples
"""
top_topics = [(0, 0)]
while top_topics[0][1] < 0.97:
lm = LdaModel(corpus=corpus, id2word=dictionary)
coherence_values = {}
for n, topic in lm.show_topics(num_topics=-1, formatted=False):
topic = [word for word, _ in topic]
cm = CoherenceModel(topics=[topic], texts=train_texts, dictionary=dictionary, window_size=10)
coherence_values[n] = cm.get_coherence()
top_topics = sorted(coherence_values.items(), key=operator.itemgetter(1), reverse=True)
return lm, top_topics
lm, top_topics = ret_top_model()
print(top_topics[:5])
Inference¶
We can clearly see below that the first topic is about cinema, second is about email malware, third is about the land which was given back to the Larrakia aboriginal community of Australia in 2000. Then there's one about Australian cricket. LDA as LSI has worked wonderfully in finding out the best topics from within LDA.
pprint([lm.show_topic(topicid) for topicid, c_v in top_topics[:10]])
lda_lsi_topics = [[word for word, prob in lm.show_topic(topicid)] for topicid, c_v in top_topics]
Evaluating all the topic models¶
Any topic model which can come up with topic terms can be plugged into the coherence pipeline. You can even plug in an NMF topic model created with scikit-learn.
lsitopics = [[word for word, prob in topic] for topicid, topic in lsitopics]
hdptopics = [[word for word, prob in topic] for topicid, topic in hdptopics]
ldatopics = [[word for word, prob in topic] for topicid, topic in ldatopics]
lmtopics = [[word for word, prob in topic] for topicid, topic in lmtopics]
lsi_coherence = CoherenceModel(topics=lsitopics[:10], texts=train_texts, dictionary=dictionary, window_size=10).get_coherence()
hdp_coherence = CoherenceModel(topics=hdptopics[:10], texts=train_texts, dictionary=dictionary, window_size=10).get_coherence()
lda_coherence = CoherenceModel(topics=ldatopics, texts=train_texts, dictionary=dictionary, window_size=10).get_coherence()
lm_coherence = CoherenceModel(topics=lmtopics, texts=train_texts, dictionary=dictionary, window_size=10).get_coherence()
lda_lsi_coherence = CoherenceModel(topics=lda_lsi_topics[:10], texts=train_texts, dictionary=dictionary, window_size=10).get_coherence()
def evaluate_bar_graph(coherences, indices):
"""
Function to plot bar graph.
coherences: list of coherence values
indices: Indices to be used to mark bars. Length of this and coherences should be equal.
"""
assert len(coherences) == len(indices)
n = len(coherences)
x = np.arange(n)
plt.bar(x, coherences, width=0.2, tick_label=indices, align='center')
plt.xlabel('Models')
plt.ylabel('Coherence Value')
evaluate_bar_graph([lsi_coherence, hdp_coherence, lda_coherence, lm_coherence, lda_lsi_coherence],
['LSI', 'HDP', 'LDA', 'LDA_Mod', 'LDA_LSI'])
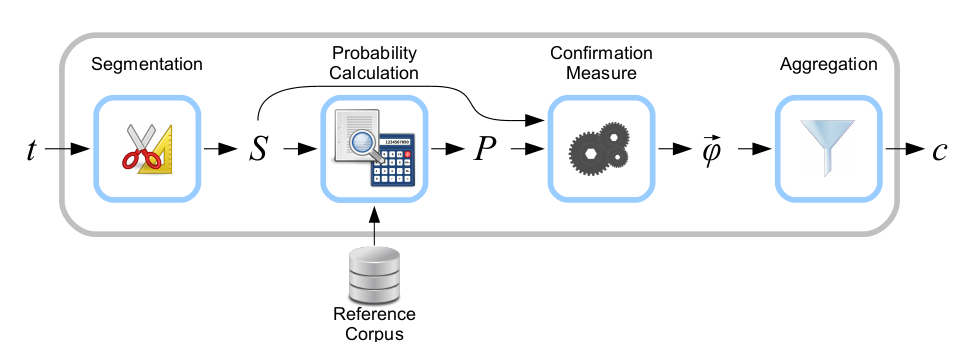
Customizing the topic coherence measure¶
Till now we only used the c_v coherence measure. There are others such as u_mass, c_uci, c_npmi. All of these calculate coherence in a different way. c_v is found to be most in line with human ratings but can be much slower than u_mass since it uses a sliding window over the texts.
Making your own coherence measure¶
Let's modify c_uci to use s_one_pre instead of s_one_one segmentation
from gensim.topic_coherence import (segmentation, probability_estimation,
direct_confirmation_measure, indirect_confirmation_measure,
aggregation)
from gensim.matutils import argsort
from collections import namedtuple
make_pipeline = namedtuple('Coherence_Measure', 'seg, prob, conf, aggr')
measure = make_pipeline(segmentation.s_one_one,
probability_estimation.p_boolean_sliding_window,
direct_confirmation_measure.log_ratio_measure,
aggregation.arithmetic_mean)
To get topics out of the topic model:
topics = []
for topic in lm.state.get_lambda():
bestn = argsort(topic, topn=10, reverse=True)
topics.append(bestn)
Step 1: Segmentation
# Perform segmentation
segmented_topics = measure.seg(topics)
Step 2: Probability estimation
# Since this is a window-based coherence measure we will perform window based prob estimation
per_topic_postings, num_windows = measure.prob(texts=train_texts, segmented_topics=segmented_topics,
dictionary=dictionary, window_size=2)
Step 3: Confirmation Measure
confirmed_measures = measure.conf(segmented_topics, per_topic_postings, num_windows, normalize=False)
Step 4: Aggregation
print(measure.aggr(confirmed_measures))
How this topic model can be used further¶
The best topic model here can be used as a standalone for news article classification. However a topic model can also be used as a dimensionality reduction algorithm to feed into a classifier. A good topic model should be able to extract the signal from the noise efficiently, hence improving the performance of the classifier.